[10000ダウンロード済み√] (p ∧ q) → (p ∨ q) truth table 172406-(p^q)p v → (pvq)^ q truth table
WebQ Statement 1 The statement (p∨q)∧∼p and ∼p∧q are logically equivalent Statement 2 The end columns of the truth table of both statements are identical Q In a cyclicWeb¬ (p ∧ q) ∨ ¬ (p ∨ q) (p ↔ ¬q) ⊕ (p → q) Determine whether the following statements are logically equivalent using truth tables ¬ (p → q) and (p ⊕ ¬q) (p ∧ q) → r and p ↔ (q → r)WebProof using Truth Table Friday, Chittu Tripathy Lecture 05 Modus Tollens Example Let p be "it is snowing" Let q be "I will study discrete math" "If it is snowing,

Use A Truth Table To Determine Whether The Following Statement Is A Contradiction A Tautology Or Brainly Com
(p^q)p v → (pvq)^ q truth table
(p^q)p v → (pvq)^ q truth table-0 0 Similar questions Construct theWebWhatis%logic?% Logic is a truthpreserving system of inference Inference the process of deriving (inferring) new statements from old statements System a set of mechanistic



Answer In Discrete Mathematics For Angelica Aguilar
Web Teams Q&A for work Connect and share knowledge within a single location that is structured and easy to search Learn more about TeamsWeb CS 536 Science of Programming Mon , 1350 Practice 1 15 (p is a tautology) and (¬p is a contradiction) are equivalent;Webq You will have an exam next day;
See the answer Construct truth table for each of the following compound statements (a) (p ∨ q) ∧ ¬ (p ∨ q) (b) (p ∨ q) → (¬p ∧ q) (c) (¬p ∧ q)WebVerified answer Yes, it is a tautology You could construct a truth table to see this, but a better way is to think about when it could be false For an implication to be false, the leftWebUsing the truth table, verify p → (p → q) ≡ ~ q → (p → q) Advertisement Remove all ads Solution In the above truth table, entries in columns 5 and 6 are identical ∴ p → (p → q) ≡
Web a) p → q b) ¬q ↔ r c) q → ¬r d) p ∨ q ∨ r e) (p → What is discrete mathematocs and application Make a Fully truth table and identify if it is a tautology, contradiction,0 0 Similar questions The truth values of p,q and r for which (p∧q)∨(∼r)WebBy looking at the truth table for the two compound propositions p → q and ¬q → ¬p, we can conclude that they are logically equivalent because they have the same truth values (check



Solved Subject Discrete Structures Show By The Use Of The Truth Course Hero
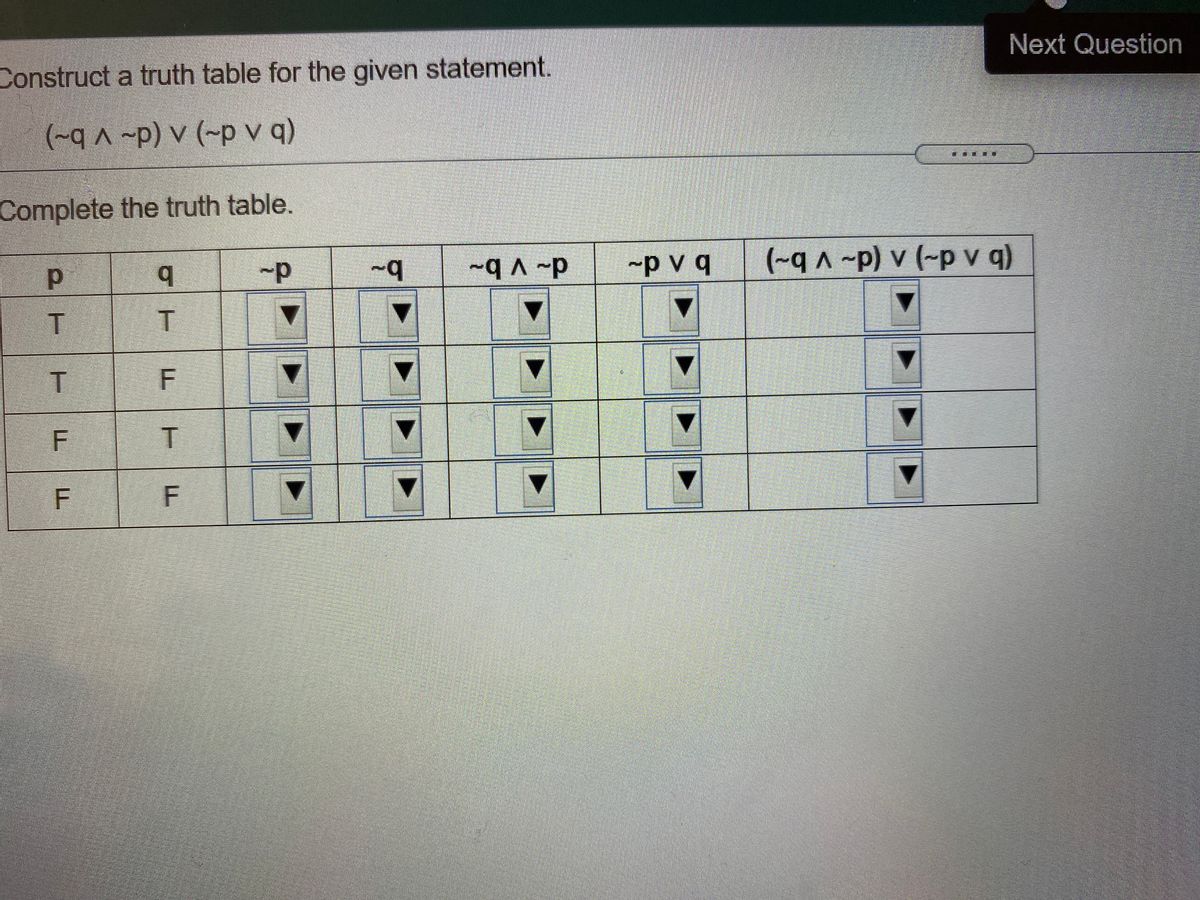



Answered Construct A Truth Table For The Given Bartleby
WebA Click to see the answer Q Use laws and logical equivalences of propositional logic to show that (p ∧ q) → p is a tautology A Given that, p∧q→p Q 22 Show that (p ^ q) → (p V q) is aWeb(p↔~q)⇒(~p∧q)∨(p∧~q) ((p↔~q)⇒(~p∧q)∨(p∧~q)) CNF, DNF, truth table calculator, logical equivalence generator THERE'S THE ANSWER!WebF F F In the above table, entries in columns 5, 7, and 8 are identical ∴ ~ (p → ~q) ≡ p ∧ ~ (~ q) ≡ p ∧ q Email ThisBlogThis!Share to TwitterShare to FacebookShare to Newer



Truth Tables Tautologies And Logical Equivalences




Discrete Mathematics How To Compute Cnf From Truth Table Mathematics Stack Exchange
WebHow to Construct a Truth Table Example with ~p ^ (q V ~r)If you enjoyed this video please consider liking, sharing, and subscribingUdemy Courses Via My WebWeb Two logical statements are logically equivalent if they always produce the same truth value Consequently, p≡q is same as saying p⇔q is a tautology Beside distributiveWebQuestion Construct the truth table of the following (∼p∨q)∧(q→r)→(p→r) Easy Open in App Solution Verified by Toppr Was this answer helpful?




Discrete Mathematics Using A Truth Table To Prove Or Disprove P Vee Q Wedge R P Wedge Q Vee R And P Wedge Q Vee R P Vee Q Vee R Mathematics Stack Exchange



Solved Build A Truth Table For The Following Compound Statement P Course Hero
Web3 如 g,h 是公式,则(g ∧ h)、(g ∨ h)、(g → h)、(g h)也是公式;(如:p ∧ q,(¬q) → r, ) 4 仅由有限步使用规则 (1)、(2)、(3)后所得到的包含命题变元、联结词和括号的符号串才是命 题3 2 4 2 * 8 For logic statements From highest toWebShow that ¬ q → ( p ∧ r ) ≡ (¬ q → r ) ∧ ( q ∨ p) Show the equivalence by establishing a sequence of equivalences You can only use the equivalences in lecture slides Show your



Solved Construct A Truth Table For Each Of These Compound Propositions A P Q R B P Q R C P Q R D P Q R E P Q R F P Q R



Explain Without Using A Truth Table Why Math P Neg Q Q Neg R R Neg P Math Is True When P Q And R Have The Same Truth Value And It
Web Use the truth table to determine whether the statement ((¬ p) ∨ q) ∨ (p ∧ (¬ q)) is a tautology asked in Discrete Mathematics by Anjali01 ( 481k points)Order of operations In math?WebTruth Table Generator This tool generates truth tables for propositional logic formulas You can enter logical operators in several different formats propositional formula p ∧ q →




Truth Tables Brilliant Math Science Wiki




Truth Tables Of Five Common Logical Connectives Or Operators Chilimath
WebIf P is false, we look at (Q→P) Note that if Q is true, we have true implies false, which is false Therefore, when P is false and Q is true, the proposition P∨ (Q→P) is false and thus is not aWeb (1) Truth Tables For one, we may construct a truth table and evaluate whether every line in the table is in fact true This is fine when the statement is relativelyWeb11 PROPOSITIONS 7 p q ¬p p∧q p∨q p⊕q p → q p ↔ q T T F T T F T T T F F F T T F F F T T F T T T F F F T F F F T T Note that ∨ represents a nonexclusive or, ie, p∨ q is true when any



Solved Construct The Truth Table For Each Of The Following Compound Course Hero




Solved Complete The Following Truth Table By Filling In The Chegg Com
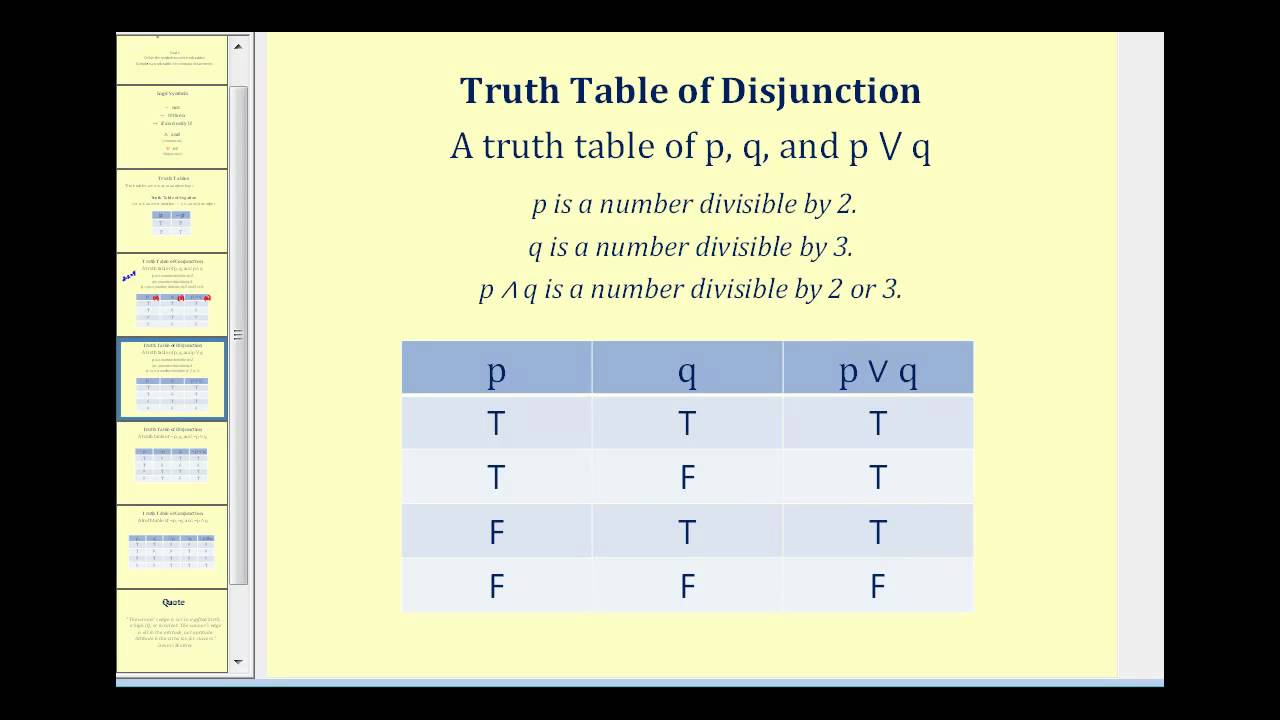
WebI'll do it in blue Notice there are no cases of T on the left and F on the right, so they're all T's Case (p → q) ∧ p → q 1 T T T 2 F T F 3 F T T 4 F T F Finally erase the two columns thatWebTruth Table for Disjunction of p and q (p V q)If you enjoyed this video please consider liking, sharing, and subscribingUdemy Courses Via My Website httpWeb(p→(q→r))↔((p ⋀ q)→r) 3 (p ∨ ~r)→( ~q ∧ s) 1 Use truth tables to verify the associative law (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) The two propositions (p ∨ q) ∨r and p∨ (q∨r) are equivalent,



Answer In Discrete Mathematics For Angelica Aguilar




Using The Truth Table Prove The Following Logical Equivalence P Q R P Q P R
Web(P→Q)∧ (Q⇔P) ( (P→Q)∧ (Q⇔P)) CNF, DNF, truth table calculator, logical equivalence generator THERE'S THE ANSWER! Mister Exam Mathematical logic signs and operationsWebClick here to add your own comments Truth Table by Staff Answer Your problem statement shows the following Boolean expression ~ (p → r) ∧ q which can alsoWebOriginally Answered How do you prove that (p ∨ q) ∧ (¬p ∨ r) → (q ∨ r) is a tautology?




Solved Construct A Truth Table For Each Of These Compound Propositions A P P B P P C P P Q D P Q P Q E Q P P Q F P




Solved Are P Q R And P Q P R Logically Chegg Com
Web1 First, I'll say that the paragraph implicitly uses truth tables to compare the cases where P > Q and ~P v Q, finding them to be the same Any statement that can be proven with aWeb(Complement Law) ≡ (∼ p ∧ ∼ q) ∨ (q ∧ p) (Identity Law) ≡ (∼ p ∧ ∼ q) ∨ (p ∧ q) (Commutative Law) ≡ (p ∧ q) ∨ (∼ p ∧ ∼ q) (Commutative Law) ≡ RHS ConceptWeb If (p ∧ q) is true, then both p and q are true, so (p ∨ q) is true, and T → T is true If (p ∧ q) is false, then (p ∧ q) → (p ∨ q) is true, because false implies anything QED Share Cite Follow answered at 247 marty cohen 104k 9 69 170 1 True, but



Prove That P Q R P Q R Using Truth Table Sarthaks Econnect Largest Online Education Community




Without Using Truth Table Prove That Pvvq P Toq Is A Tautology Youtube
Webanswer Simplificar la proposición (p ∨ q) ∨ (p ∧ q) → (p ∧ q)WebFor example, the compound statement P → (Q∨ ¬R) is built using the logical connectives →, ∨, and ¬ The truth or falsity of P → (Q∨ ¬R) depends on the truth or falsity of P, Q, and R AWeb1 day ago Compound truth tables Consider ¬p ∧ q ∨ r> what operation do we do first?



Answer In Discrete Mathematics For Angelica Aguilar



Answer In Discrete Mathematics For Angelica Aguilar
WebExplanation for Correct Option p → ( p ∧ ~ q) is False The table shows that we get false only when p and q will be TT ∴ p → ( p ∧ ~ q) is false when p is true and q is true Hence OptionWeb(p →q)∧(q →r)∧p ⇒r We can use either of the following approaches Truth Table A chain of logical implications Note that if A⇒B andB⇒C then A⇒C MSU/CSE 260 Fall 09 10 Does (pA Truth table is always the easy answer to these questions Be we can also apply logic the
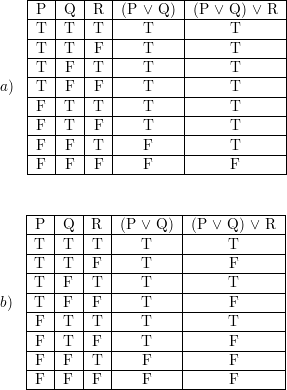



Construct A Truth Table For Each Of These Compound Propositi Quizlet
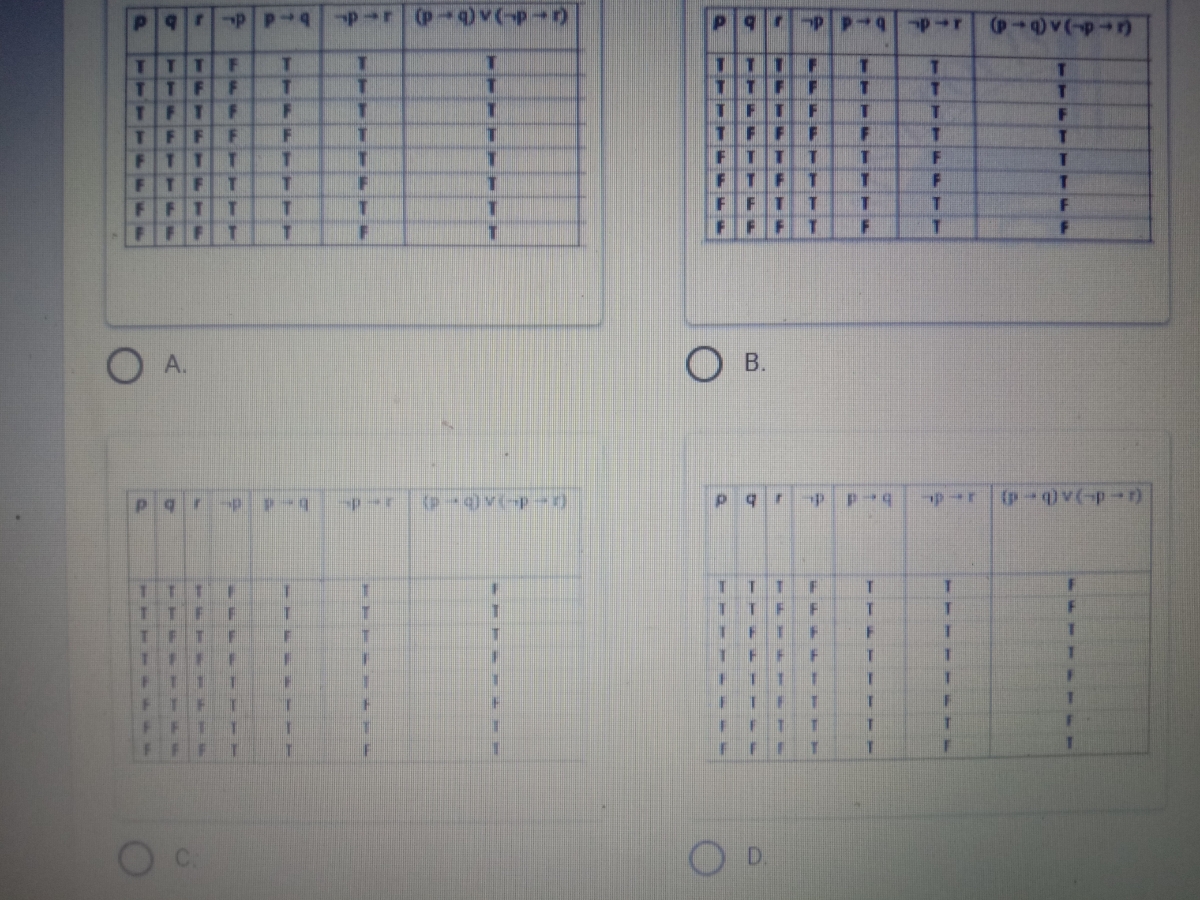



Answered Identify The Correct Truth Table That Bartleby
P ∨ q p q FALLACY OF THE INCLUSIVE OR Thus, it's INVALID If we search the Internet, then we will find information about logic We searchedWebConstruct the truth table for (p∧q)∨∼(p∧q) Medium Solution Verified by Toppr Was this answer helpful?WebThe truth tables of every statement have the same truth variables Example Prove ~ (P ∨ Q) and (~P) ∧ (~Q) are equivalent Solution The truth tables calculator perform testing by



Solved Construct Truth Tables For The Statement Forms In 5 11 P Q R P Q R



Proof And Problem Solving Truth Table Example 02 Youtube
WebAnswer (1 of 2) ~(p/\q)V(p V q) =1 details From De Morgan's theorem ~(p /\ q) = (~p V ~q) Thus ~(p/\q)V(p V q) = (~p V ~q) V( p V q) This expression is always true since not p orWeb All the entries in the last column of the above truth table are T ∴ (p ∧ (p → q) → q is a tautology (p ∧ q) ∨ (~p ∧ ~q) (ii) (p ∧ q) → r ≡ p → (q → r) asked inWebThis problem has been solved!



Using Truth Tables Prove The Following Logical Equivalences P Q P Q Q P Sarthaks Econnect Largest Online Education Community




Using The Truth Table Prove The Following Logical Equivalence P Q P Q P Q
So are (p is a contingency) and (¬pis aWebGive a semiformal Natural Deduction proof of the following claim You may only usethe eight Natural Deduction rules and no equivalence rules (such as De Morgan's Laws)Claim (R ∧S)WebStatement −2 r 2 = ∼ (p ↔ ∼ q) = (p ∧ q) ∨ (∼ q ∧ ∼ p) From the truth table of r, r1 and r2, r = r1 Hence Statement − 1 is true and Statement −2 is false 152 Views Answer since p ∨ ~



Show That P Q And P Q Are Logically Equivalent Quora




Discrete Mathematics How Do I Prove That P To Q Wedge R And P To Q Wedge P To R Are Logically Equivalent Mathematics Stack Exchange
Web (a) (p → q) → r (b) (p ∧ For each of the given statements 1 Express each of the statements using quantifiers and propositional functions 2 Form the negation of theWeb1 P∧Q Assumptions 2 Q∨R 3 R→ ¬P 4 P ∧elim 1 5 Q ∧elim 1 6 ¬Q ∨elim assumption 2 7 Contra Contraelim 5,6 8 R ∨elim assumption 2 9 ¬P →elim 3,8 10 Contra Contraelim 4,9




Proof And Problem Solving Truth Table Example 02 Youtube



Answer In Discrete Mathematics For Ahmed 994




Propositional Calculus Verifying Logic Without Drawing Truth Tables Mathematics Stack Exchange




Discrete Mathematics Using A Truth Table To Prove Or Disprove P Vee Q Wedge R P Wedge Q Vee R And P Wedge Q Vee R P Vee Q Vee R Mathematics Stack Exchange
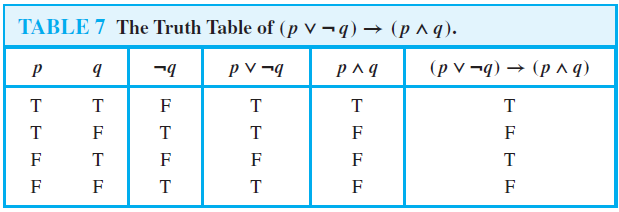



Q Ise P Solved 26 Show That P Q R And Q P V R Are Chegg Com Northdevonpermaculture Com




Logic Truth Table For P Q R Q Youtube




Solved Complete The Truth Table For The Following Compound Statement P 9 P V 9 P Q P 4 Pv Q T T 2 2 P
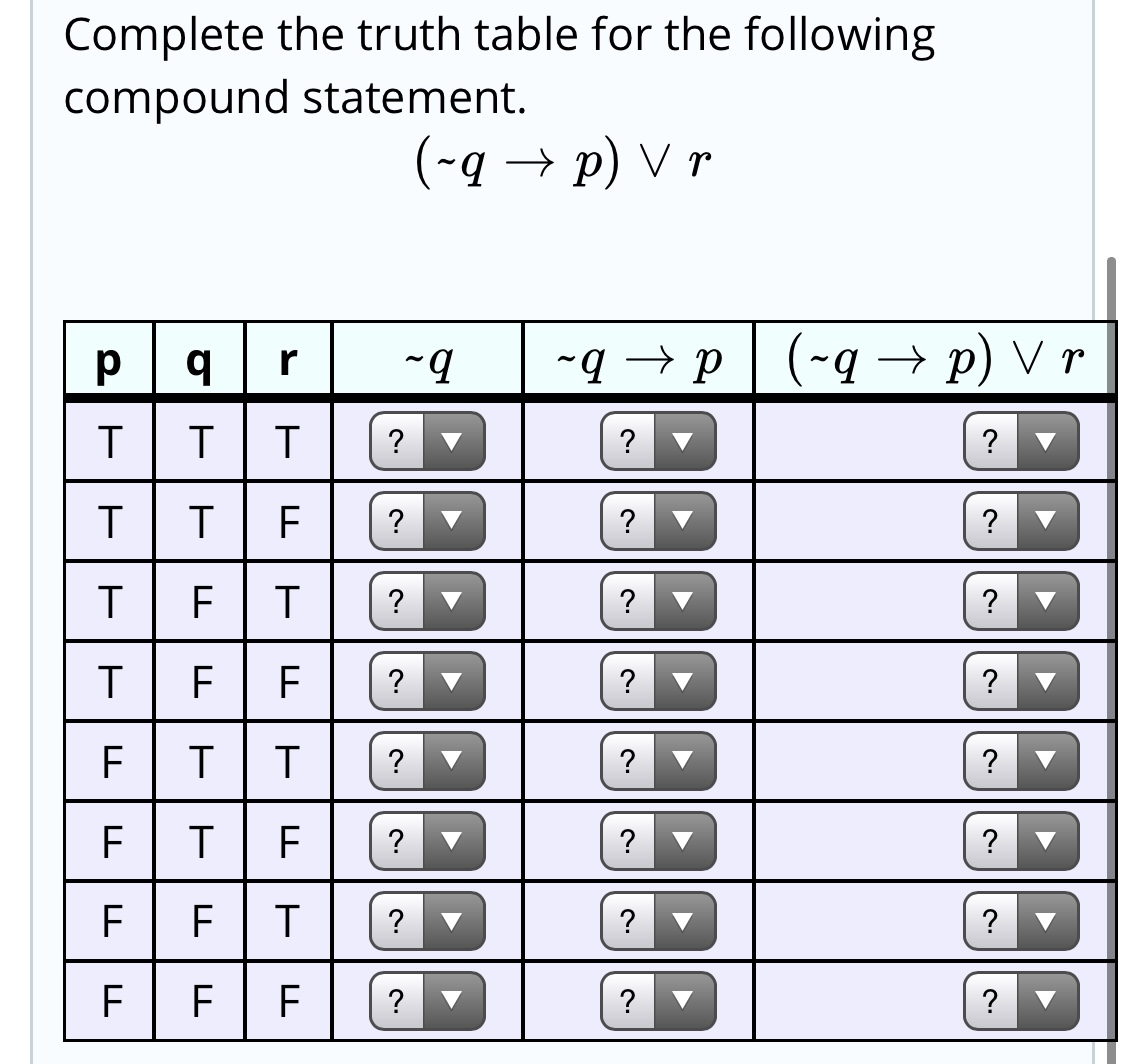



Answered Complete The Truth Table For The Bartleby




Construct A Truth Table For P Q P Q Q Brainly In




Solved Construct A Truth Table For Each Of These Compound Propositions A P Q R B P Q R C P Q P R D P Q P R E P Q Q




Construct A Truth Table For Each Of These Compound Propositi Quizlet




Logic Truth Table For P Q R Q Youtube



Truth Tables For Compound Statements Youtube



Solved Complete The Truth Table For The Following Compound Chegg Com




Logic Part 3 Truth Tables Ethical Realism




Construct A Truth Table For The Following Statement Form P Q R P N Q R Brainly In




Truth Tables Of Five Common Logical Connectives Or Operators Chilimath




What Is The Truth Table For P Q Q R P R Quora




Discrete Mathematics Show That The Following Is A Tautology Without Using Truth Tables P To Q Wedge Q To R To P To R Mathematics Stack Exchange



Construct A Truth Table For Each Of These Compound Propositi Quizlet




Construct The Truth Tables For The Following Expressions A P Q R B P Q P R C P Brainly Com




Logic And Proofs



2




Prepare The Truth Table Of The Following Statement Patterns I P Q Q P Ii P Q P Iii P Q P Q Iv P R Q P V P Q R P




Show That Each Conditional Statement Is A Tautology Without Using Truth Tables A Neg Pwedge Pv Q To Q B P To Q Wedge Qto R To Pto R C Pwedge Pto Q To Q D



Answer In Discrete Mathematics For Shaun




Logic Prove That Neg P Wedge Q Leftrightarrow Neg P Vee Neg Q Using Truth Table Mathematics Stack Exchange




Use A Truth Table To Determine Whether The Following Statement Is A Contradiction A Tautology Or Brainly Com



Logic Proving Neg R To P Lor Neg Q To Neg P Land R To Q To Neg P Lor Q Is A Tautology Without A Truth Table Mathematics Stack Exchange



Q Tbn And9gct2vvkimysixbpqgpy5gimw2n7mzlb8c Hbx3ih2ox1f0um Btxvge8 Usqp Cau



Answered Complete The Following Truth Table P Q Bartleby
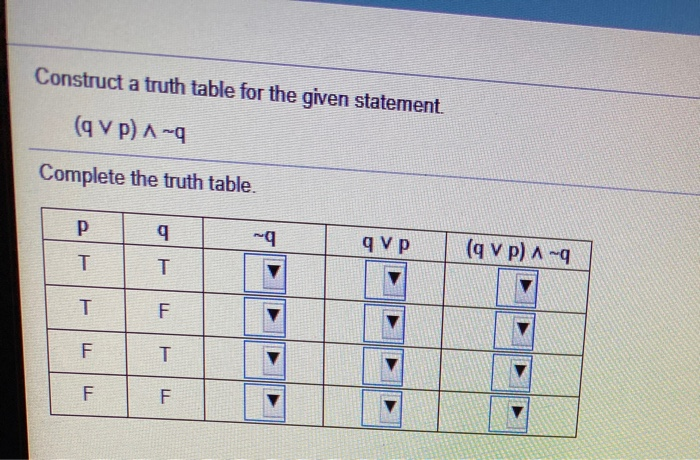



Solved Complete The Truth Table For The Given Statement By Chegg Com




In The Truth Table For The Statement P Q Q R P R Then Last Column Has The Truth Value In The Following Order Is
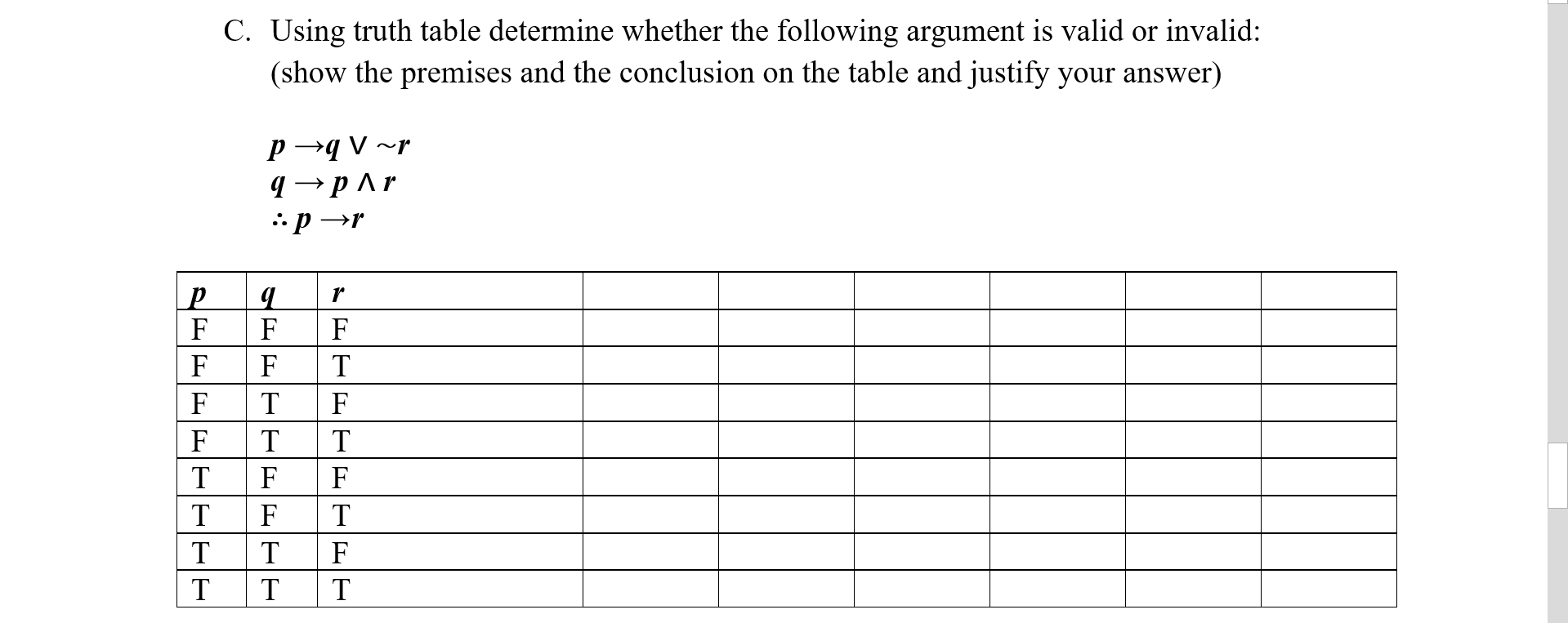



Solved Using Truth Table Determine Whether The Following Chegg Com




Truth Table For Any Proposition Tautologies Logical Equivalence Contradiction 13 Youtube



Propositional Logic Truth Table Boolean Algebra Dyclassroom Have Fun Learning




Without Using Truth Table Show That P Q P Q P Q




Construct A Truth Table For Each Of These Compound Propositions A P Rightarrow Neg P B P Leftrightarrow Neg P C P Oplus P Vee Q D P Wedge Q Rightarrow P




2 Construct The Truth Tables For The Following Propositions 1 P P Q 2 P Q Q P 3 P Q R 4 P Q P R 3 Refer To The Propositions



Q Tbn And9gcq0haky42zt0ydmhqmemkud Bgwt75qdf8x2bzfe6r7x2ic9ksao0ut Usqp Cau



Solved Construct A Truth Table For Each Of These Compound Propositions A P P B P P C P Q Q D P Q P Q E P Q Q P F P




Solved Construct The Truth Table For The Following Compound Propositions P Q P Q P Q P Q Determine Whether The Following Statements




Solved Construct A Truth Table For Each Of These Compound Propositions A P P B P Q P Q C P P Q D P Q P Q E P Q P R




Discrete Mathematics Using A Truth Table To Prove Or Disprove P Vee Q Wedge R P Wedge Q Vee R And P Wedge Q Vee R P Vee Q Vee R Mathematics Stack Exchange




Truth Tables Tautologies And Logical Equivalence



Q Tbn And9gcqcouw Yxg6rgdnhiit1mpaslm5gxbhvzqczmdq7zstpzzk3finb77n Usqp Cau



Can You Make A Truth Table Of This P L Q Quora




Answered Complete The Truth Table For The Bartleby
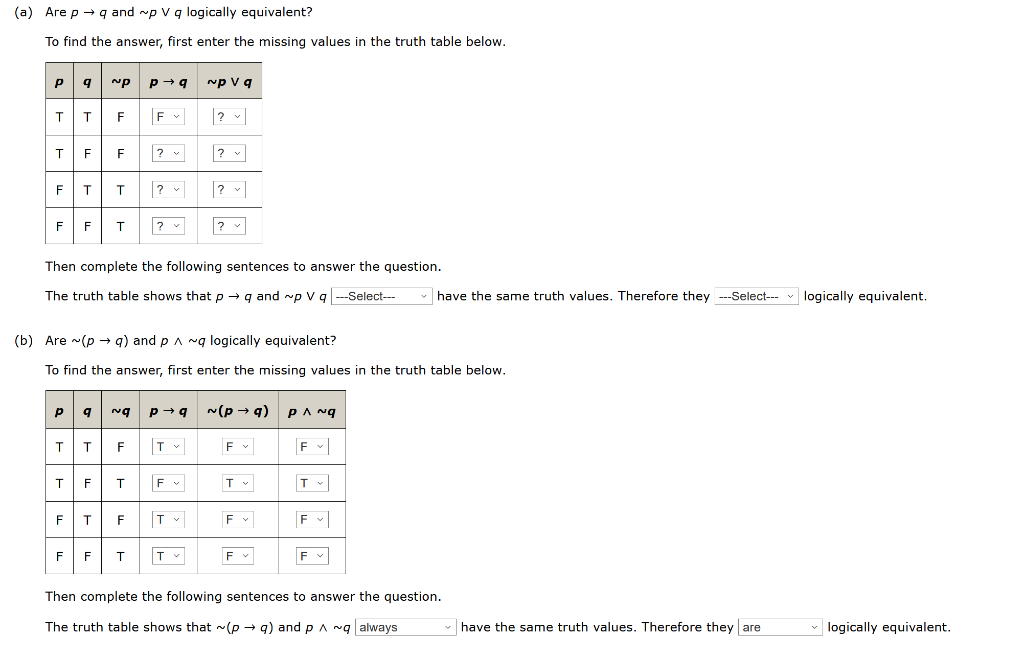



Solved A Are P Q And Wp V Q Logically Equivalent To Find Chegg Com




Construct A Truth Table For P Q R S Quizlet



Prove P Q R P Q R Without Using Truth Table Sarthaks Econnect Largest Online Education Community




Discrete Mathematics What S Wrong With This Truth Table For Implication Mathematics Stack Exchange



Solved Let A P Q R Q And B P R A Use Truth Course Hero




Truth Table 23 Free Math Worksheets
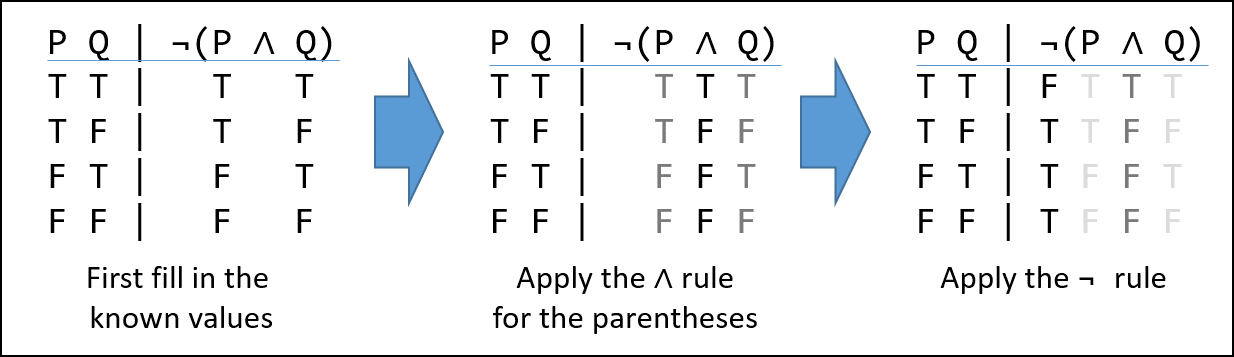



2 Circuits And Truth Tables Sireum Logika




Create A Truth Table To Determine Whether The Following Proposition Is Valid P Q P V Q Homework Study Com



2




Construct A Truth Table For Each Of These Compound Propositions A P Rightarrow Neg P B P Leftrightarrow Neg P C P Oplus P Vee Q D P Wedge Q Rightarrow P



Answer In Discrete Mathematics For Javairia 1236




Use A Truth Table To Verify The Distributive Law P Q R Quizlet




Using Truth Table Prove The Following Logical Equivalence P Q Rarr R P Rarr Q Rarr R Youtube
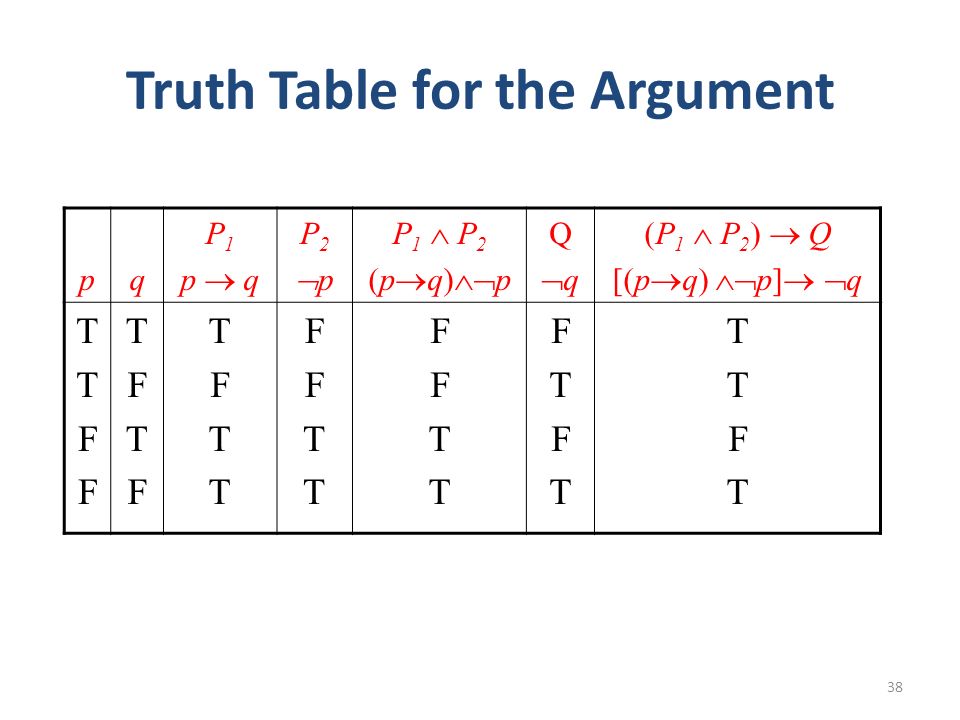



Reading Chapter 4 44 59 From The Text Book Ppt Video Online Download



Answer In Discrete Mathematics For Muhammad Abdullah 1713
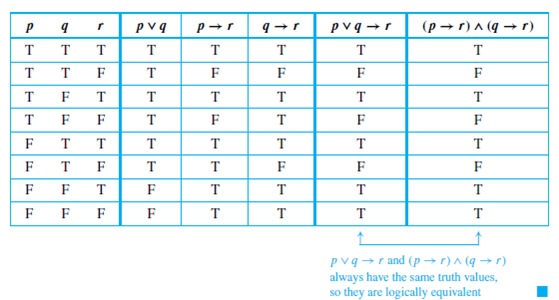



Solved Use The Logical Equivalence Established In Example To Rew Chegg Com



How To Show In A Truth Table That P Q And P Q V P Q Are Logically Equivalent Quora



What Is The Truth Table Of P Q R Q R Q Quora



Q Tbn And9gcshn1px73egmisphvbxg3xr799xgubcujuukjoui4agd 07aapwg Bu Usqp Cau




Solved P Q R Q R Q R Q P Par Chegg Com




Propositional Logic Truth Table Boolean Algebra Dyclassroom Have Fun Learning




The Foundations Logic And Proofs Ppt Download




2 Construct The Truth Tables For The Following Propositions 1 P P Q 2 P Q Q P 3 P Q R 4 P Q P R 3 Refer To The Propositions
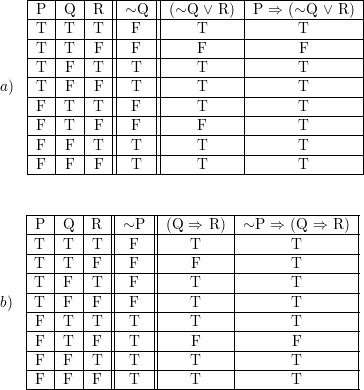



Construct A Truth Table For Each Of These Compound Propositi Quizlet



2
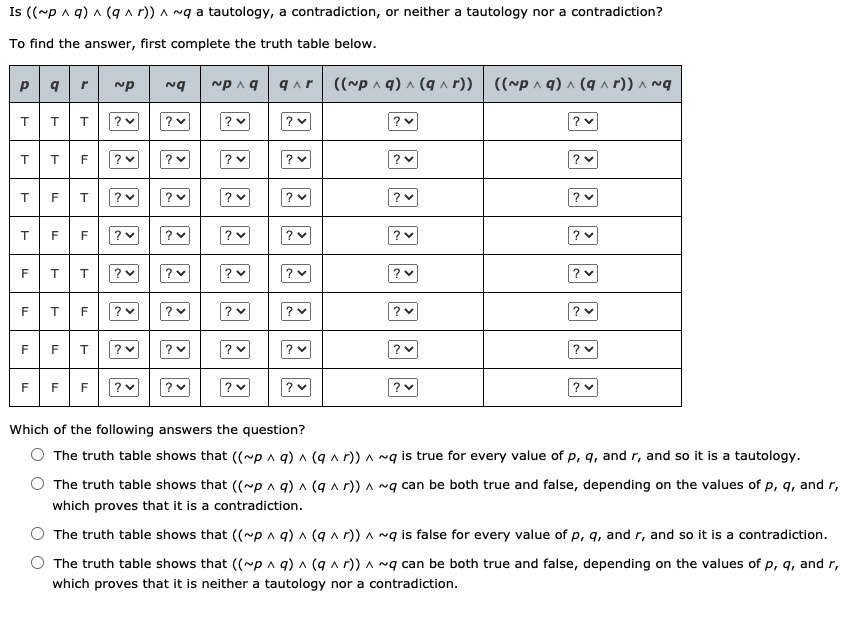



Solved Is P Q Q R Q Tautology Contradiction Or Neither Tautology Nor Contradiction To Find The Answer First Complete The Truth Table Below P Q P




Truth Table Examples Rules How To Make A Truth Table Video Lesson Transcript Study Com



Answer In Discrete Mathematics For Angelica Aguilar
コメント
コメントを投稿