√完了しました! 平面 点 距離 300955-3次元 平面 点 距離
平面・空間図形 kaztastudy 中1 作図3辺から等しい距離にある点の作図方法とは?
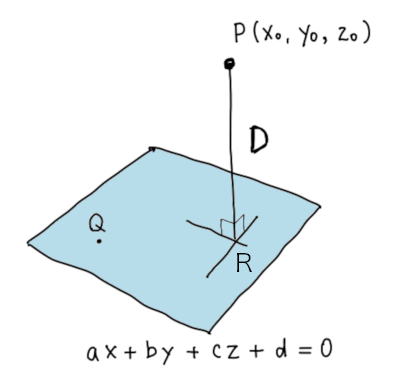
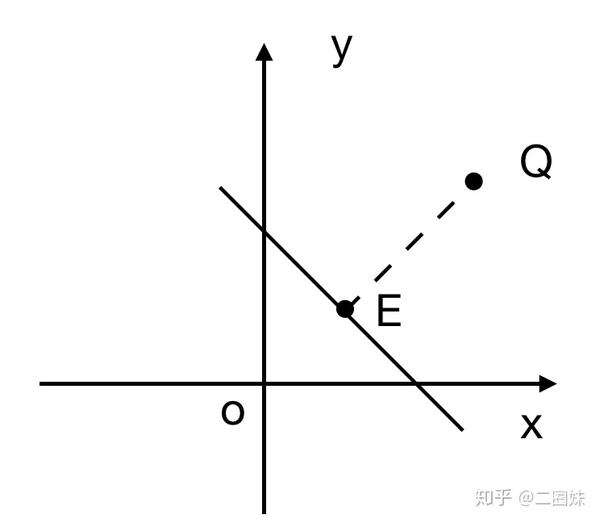
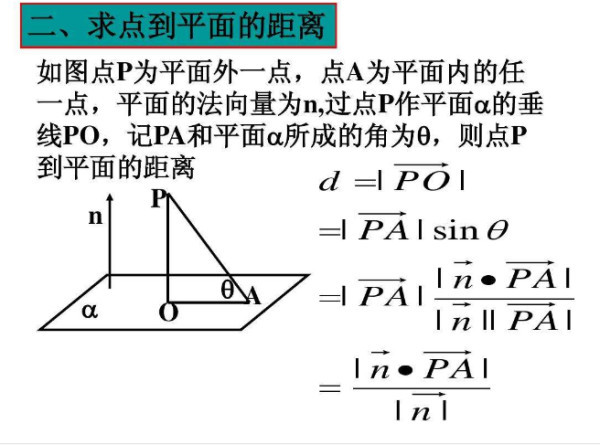
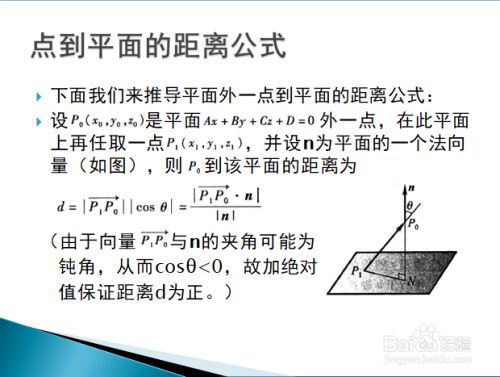
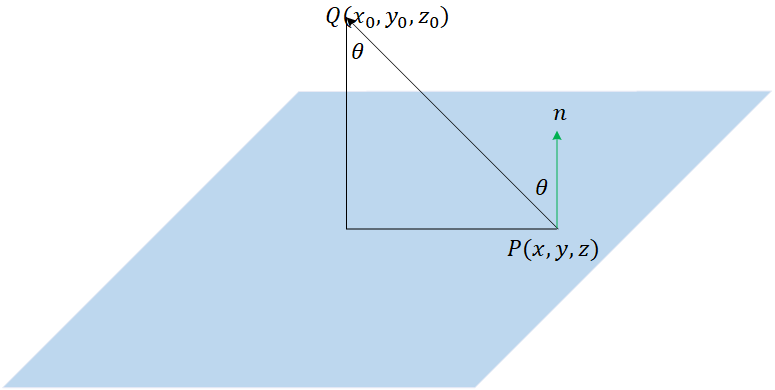
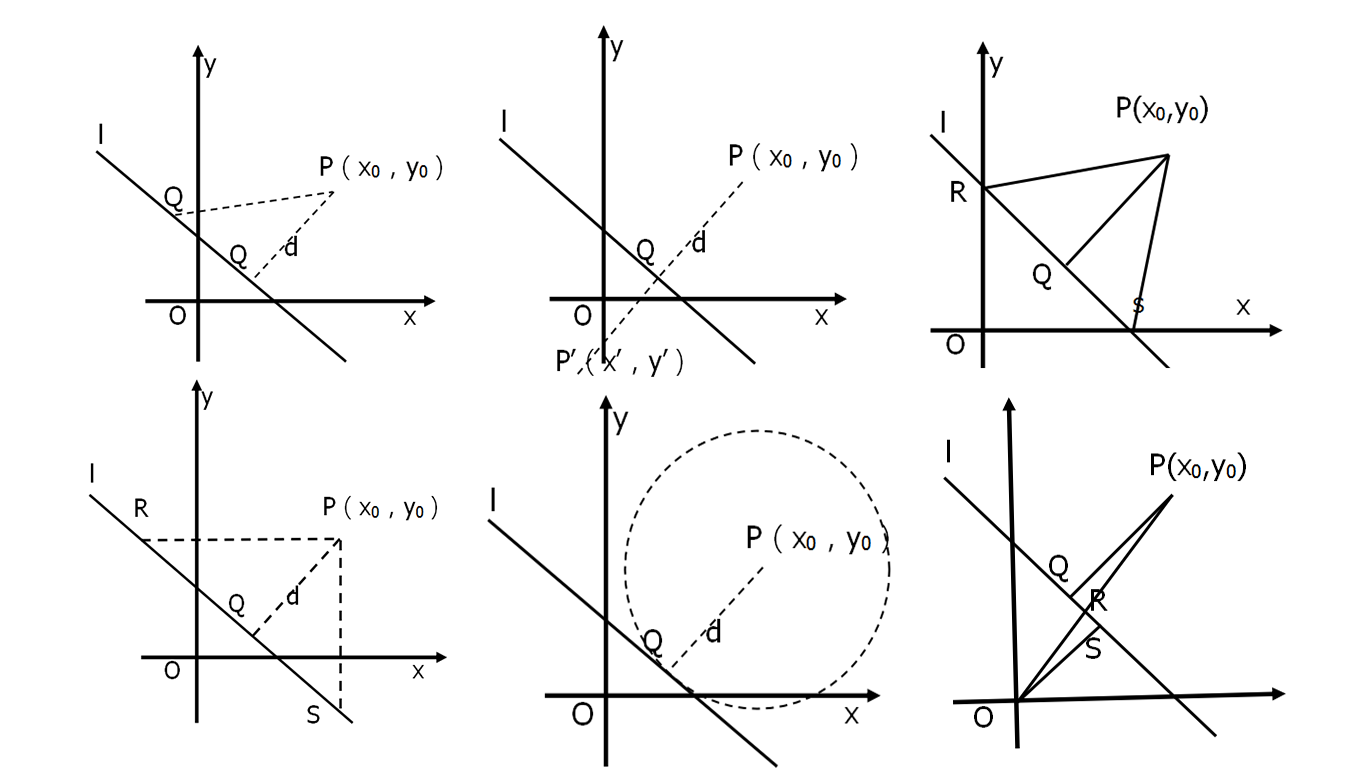
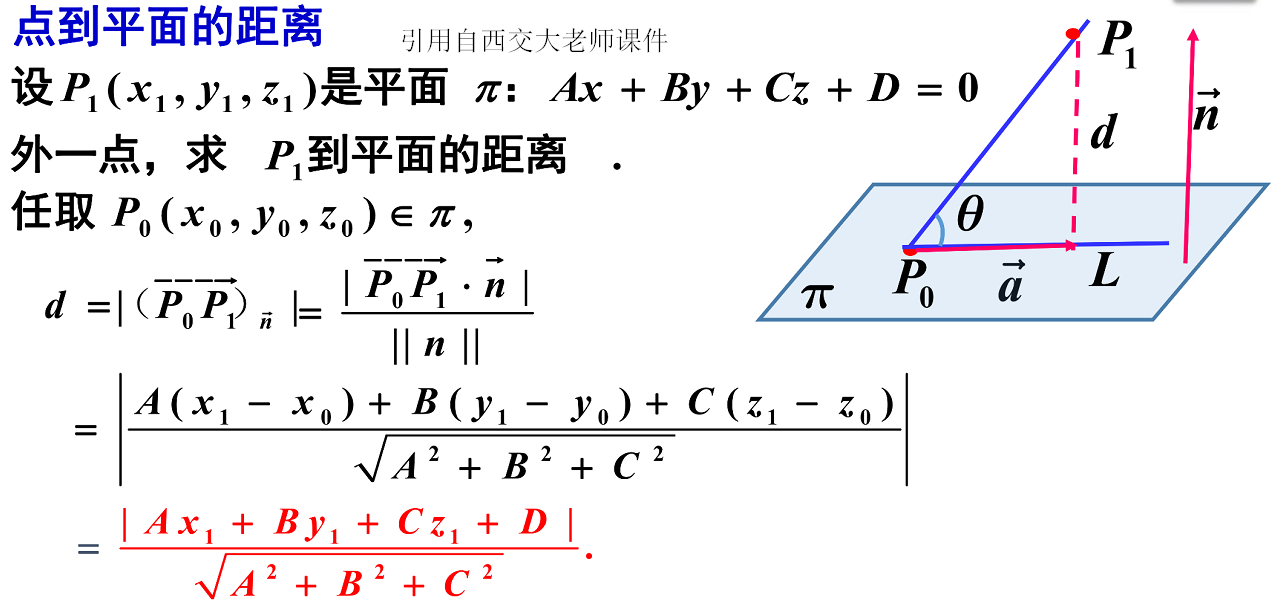
3次元 平面 点 距離-点と平面の距離の公式 座標平面における点と直線の距離の公式を復習しよう 点A(x0;y0)と直線ℓ axbyc = 0 の距離は jax0 by0 cj p a2 b2 であった 座標空間における点と平面の距離についても類似の式が成り立つ: 定理1方位角 (azimuth) φ は基準平面上の基準方向と原点から点 P の基準平面への正射影へ結んだ直線との間の角;
3次元 平面 点 距離のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
 | ||
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  |  |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
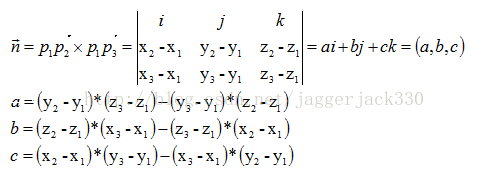 | ||
 |  | |
 |  |  |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
 |  |  |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
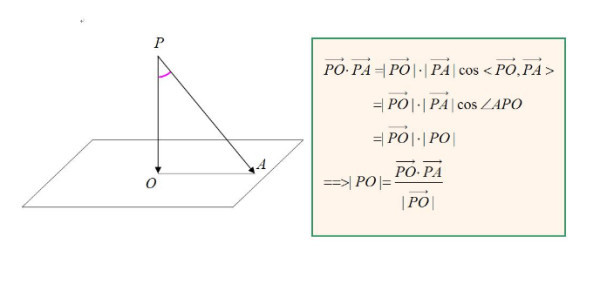 | 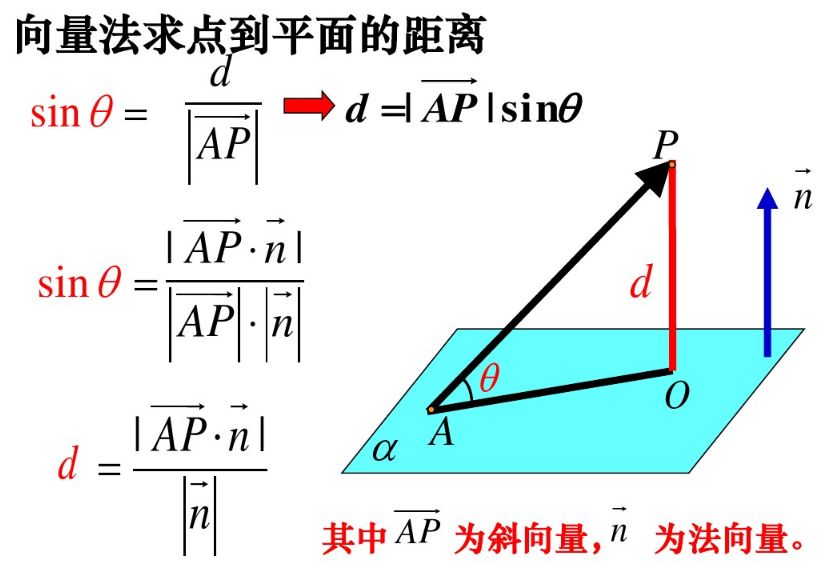 | |
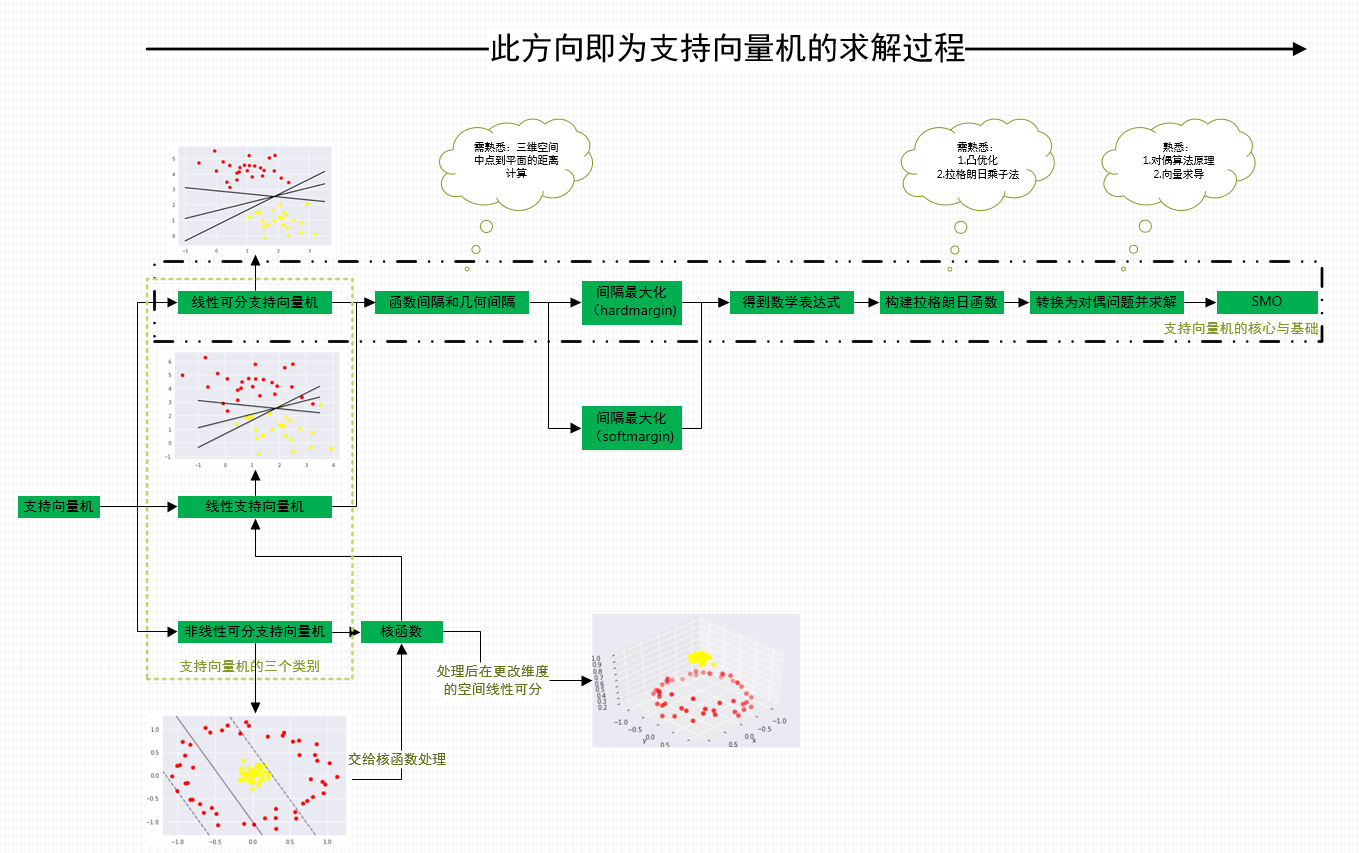
向量的点积(内积) 给定两个向量V1(x1, y1, z1)和V2(x2, y2, z2)则他们的内积是 V1V2 = x1x2 y1y2 z1z2 点到平面的距离 有了上面的准备知识,则求点到直线的距离不再是难事,有图有真相 如果法相量是单位向量的话,那么分母为1 ORGE中的实现 顺便看一下Ogre中的实现ポイントの解説授業 今回のテーマは、 空間における2点間の距離 です。 xy平面での2点間の距離については、数学Ⅱの第3章「図形と方程式」で学習しましたね。 復習 空間図形では、xy平面だけでなくz平面も登場します。 z平面 は xy平面に垂直な平面 でx,y,zの3つの平面により空間をつくります。 xyz空間における2点間の距離はどのように変化するのでしょうか? z座標についても考える さっ
Incoming Term: 平面 点 距離, 平面 点 距離 プログラム, 平面 点 距離 ベクトル, 平面 点 距離 計算, 平面 点 距離 python, 平面 点 距離 内積, 3次元 平面 点 距離,
コメント
コメントを投稿